
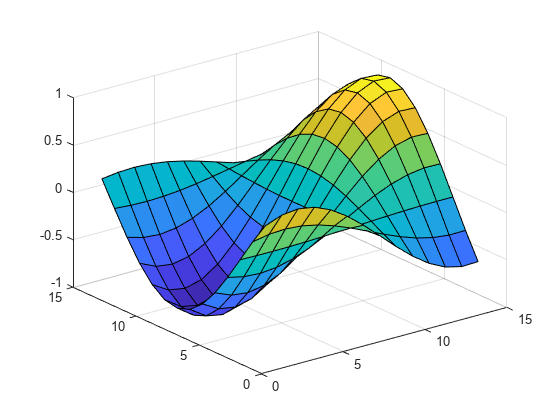
We selected cubic interpolation and our choice is reflected as follows: theinterpolationmethod = F.Method The interpolation technique is represented by the Method property. For example to inspect a 4-by-5 interval: first4x5values = F.Values(1:4, 1:5) You can access the values using standard MATLAB syntax to index into the data. The values at the grid points are stored in the Values array. GridVectors is a cell array so we can query the contents as follows: gridvectorprop = F.GridVectors This can save memory if the grid is large. The interpolant stores the grid in the compact form of GridVectors. The interpolant F has 3 properties: The GridVectors are actually the vectors xgv and ygv we used to create the grid. The 'cubic' option specifies cubic interpolation. Since the interpolant behaves like a function we will give it the variable name F. We can create an interpolant for this data set that supports interpolation within the grid. Now generate the value data: V = generatevalues(X,Y) The grid is created from a pair of grid vectors as follows: xgv = -1.5:0.25:1.5

We can create a 2D grid and then pass it to the generatevalues function to produce values at the grid points. We will begin by defining a function that generates values for X and Y input: generatevalues = - (Y+1).^2).
GRIDDED INTERPOLATION MATLAB HOW TO
This example shows you how to create a griddedInterpolant for a gridded data set and then interpolate over a finer grid. Interpolating a Dataset in a Repeated Manner.Interpolating Grids that have Multiple Values at Each Gridpoint.Interpolating Grids in General Dimensions.Selecting a Different Interpolation Method.The following examples demonstrate how to create a griddedInterpolant and how to use it effectively to perform grid-based interpolation. The griddedInterpolant can generally outperform the INTERP1/2/3/N functions as it is able to cache and reuse the same interpolating function. In this scenario the overhead is accumulative. These improvements are readily apparent when interpolating the same grid in a repeated manner. It is designed to support the interpolation of grids in NDGRID format and leverage memory and performance advantages where possible. The griddedInterpolant class provides similar capabilities. MATLAB provides the INTERP family of functions to support interpolation on grids that are in NDGRID or MESHGRID format. Grid-based interpolation provides the functionality needed to carry out these tasks. Typically, we may need to refine the grid to improve resolution or de-refine the grid if it contains more detail than we practically need. When we work with gridded data we often need to know the values at locations other than at the grid points.

Grid-based data also fits naturally within the array-based environment MATLAB® provides. This data format represents values or intensities at discrete grid point locations. A grid is a common and useful way to organize data.


 0 kommentar(er)
0 kommentar(er)
